Case Studies

Problem

This gas turbine had history of high vibration since commissioning 20 years ago. Previous balancing attempts were largely unsuccessful. The keyphasor (KP) was unreliable making it difficult to reuse the influence coefficients. Several other problems were found with the couplings, bearing pitting, and magnetism.

Figure 1. Vibration Measurements

Multi-Plane Balancing

A temporary optical KP was installed. Vibration amplitudes and phase angles were trended over several hours. It was determined that at least 3 hours were required to stabilize the turbine vibration while generating 35 MW of power. Previous balance attempts did not allow sufficient time for heat soaking of the turbine rotor.

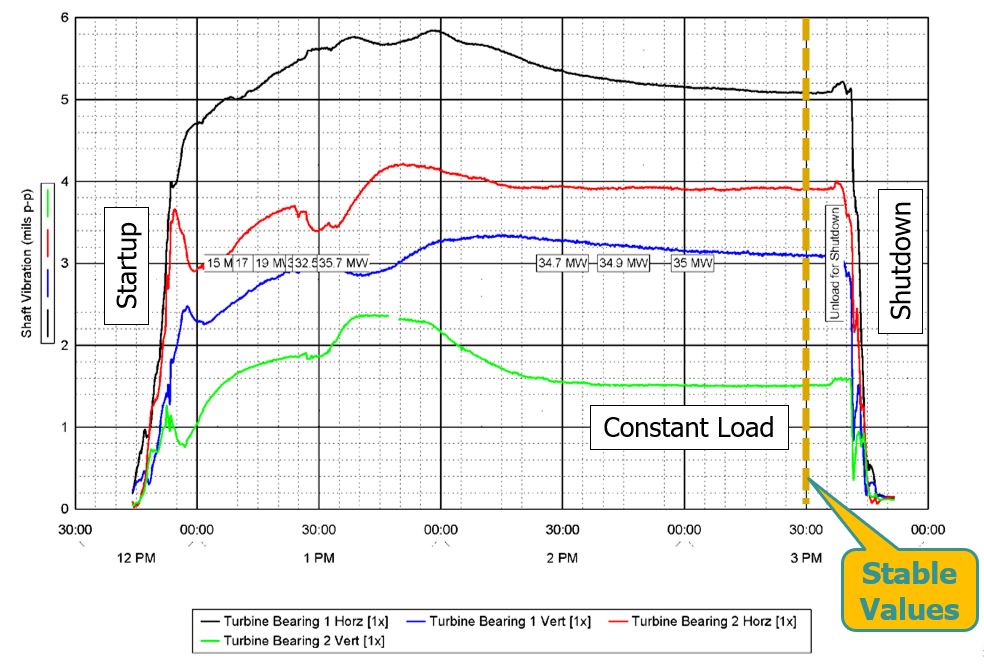
Figure 2. Vibration Trend (3-Hr Period)

Influence coefficients are determined from trial weights and vibration measurements. Goodman (1964) applied least squares and assumed linear behavior.  This method can be used with multiple balance planes and operating speeds. Predicted residuals indicate if rotor can theoretically be balanced. Influence coefficients are commonly used for dynamic balancing. Matrix operations may require calculator or computer program. Use vibration amplitude and phase at 1× running speed in multiple directions.  It is very important that runout vectors be subtracted from the proximity probe readings.

Balancing begins with obtaining baseline vibration (amplitude and phase) after machine is heat soaked and readings stabilize.  Next, install a reasonably sized trial weight and retake vibration readings. “Rule of thumb” for sizing the initial trial weight using the 10% force method.

The angular location of trial weight is typically referenced to the keyphasor, opposite shaft rotation. This is repeated for each balance plane.  For this system, balance plane 1 was the accessary coupling on the gearbox end and balance plane 2 was the load coupling on the generator end.

Figure 3. Accessary Coupling

Figure 4. Load Coupling

The influence coefficients are calculated by subtracting the baseline from the trial data and dividing by the trial weight. Then solve for the correction weight(s) needed to minimize residual vibration. After balancing, the turbine vibration was reduced from 5.1 to 1.75 mils p-p as shown in Table 1.

This can also be shown graphically with orbit plots of the shaft vibration at the bearing locations.  Figure 5 shows the as found (black) versus balanced condition (green).

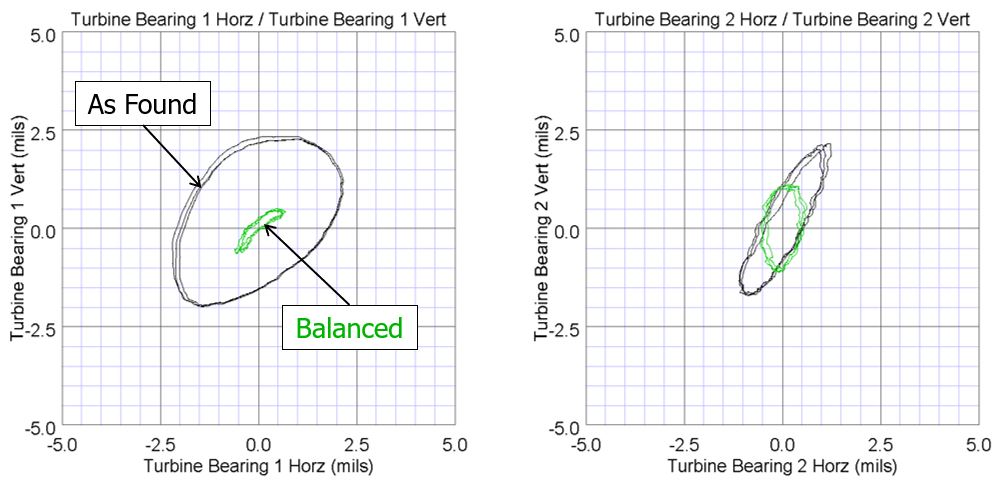
Figure 5. Orbit Plots

Conclusions

Turbine vibration is often sensitive to heat and load. During the testing, three hours were required for the vibration readings to stabilize. Even after steady readings, vibration could still vary with load. Final correction weights were installed “out-of-phase” on both ends of the turbine. This indicates sensitivity to the conical whirl mode and not the rotor midspan mode, which would have “in-phase” vibration at both bearings. Large weights were required to balance the turbine, which indicates available balance planes are at ineffective locations compared with where the actual imbalance occurs in the rotor.

References

• Feese, T., “Least Squares Balance Program for the Hewlett-Packard 48GX Calculator,” Vibrations Magazine, March 1998.
• Feese, T., “High Shaft Vibration of Synchronous Generator,” Vibrations Magazine, December 1998.
• Feese, T. D. and Grazier, P. E., “Balance This! Case Histories from Difficult Balancing Jobs,” 33rd Texas A&M Turbomachinery Symposium, September 2004.
• Fox, Randall, “Dynamic Balancing,” 9th Texas A&M Turbomachinery Symposium, 1980.
• Goodman, Thomas P., “A Least-Squares Method for Computing Balance Corrections,” J. Engrg. Indus., Trans. ASME, August 1964.
• Jackson, Charles, “Single Plane Balancing,” Texas A&M Turbomachinery Symposium, February 1991.
• MacPherson, H., Taylor, T., Feese, T., “An 11000 RPM Steam Turbine Case History,” Canadian Machinery Vibration Association, 2003.
• Shreve, Dennis, “Balancing Without Phase,” UPTIME Magazine, January 2011.
• Smith, D. R. and Wachel, J. C., “Controlling Fan Vibration – Case Histories,” EPRI Symposium on Power Plant Fans: The State of the Art, Indianapolis, Indiana, Oct. 1981.
• Wowk, Victor, Machinery Vibration: Balancing, McGraw-Hill, 1995.